红黑树

前置知识

什么是二叉查找树（BST）？

1. 左子树上所有结点的值均小于或等于它的根结点的值

2. 右子树上所有结点的值均大于或等于它的根结点的值。

3. 左、右子树也分别为二叉排序树。

   基于二分查找建树。但存在插入之后节点不平衡情况，由此引入红黑树。

红黑树是一种自平衡的二叉查找树，其具有如下特性：

1. 节点是红色或黑色
2. 根节点是黑色
3. 每个叶子节点都是黑色的空节点（NIL节点）。
4. 每个红色节点的两个子节点都是黑色。即从叶子到根不可能有两个连续的红色节点
5. 从任意节点到其每个叶子的所有路径都包含相同数目黑色节点。

典型红黑树如图：

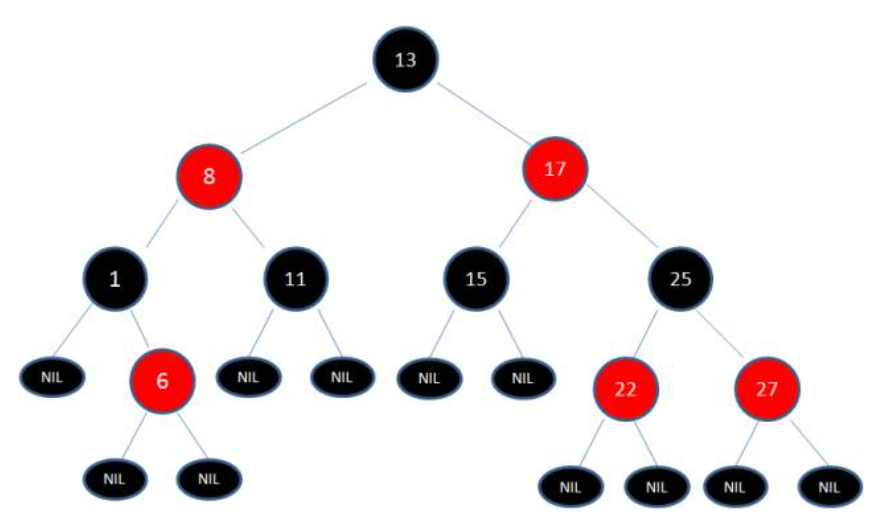
由上述构建规则限制，保证了红黑树从根到叶子的最长路径不会超过最短路径的2倍。

红黑树的调整

当插入和删除节点时，红黑树规则会被打破，此时要对其进行调整，以满足条件。调整有两种方法：变色和旋转，而旋转又分为左旋转和右旋转。

红黑树的左旋和右旋

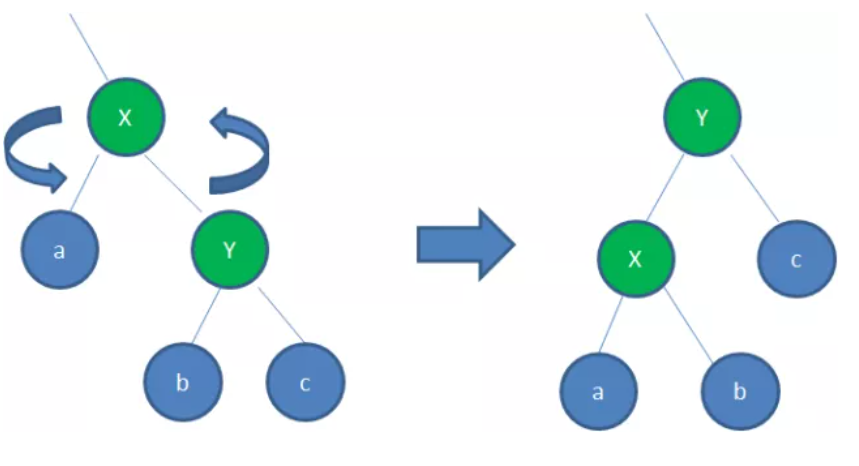
左旋即逆时针旋转红黑树的两个节点，使得父节点被自己的右孩子取代，而自己成为自己的左孩子，如图：

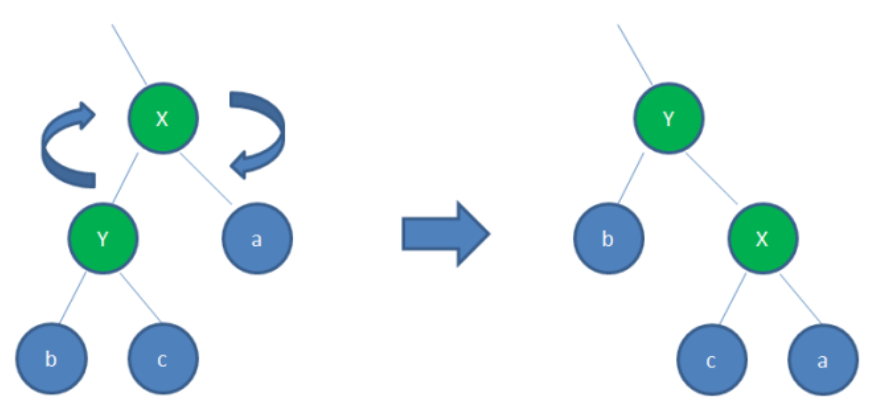
右旋即顺时针旋转红黑树的两个节点，使得父节点被自己的左孩子取代，而自己成为自己的右孩子。如图：

实际使用中，变色和旋转视情况混合使用。

红黑树的应用

在JDK的集合类TreeMap和TreeSet底层都是红黑树实现。在Java8中，HashMap也用到了红黑树.